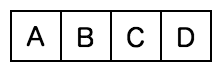Table of Contents
様々な場合の数の練習問題と解答です。問題は順次追加されます。
練習問題1
(1) 目の和が8となる場合の数
(2) 目の積が4の倍数となる場合の数
(3) 目の和または積が8となる場合の数
目の出方を数えます。目の和が8となる場合の2つのサイコロの目の出方は以下のようになります。
| サイコロ大の目 | サイコロ小の目 |
|---|---|
| 2 | 6 |
| 3 | 5 |
| 4 | 4 |
| 5 | 3 |
| 6 | 2 |
以上より、目の和が8となるときの場合の数は5通りです。
サイコロの目の積の最大値が36であることから、その範囲内で出る可能性のある4の倍数と、その時の目の出方を考えます。
| 4の倍数 | サイコロ大 | サイコロ小 |
|---|---|---|
| 4 | 2 | 2 |
| 8 | 2 | 4 |
| 4 | 2 | |
| 12 | 2 | 6 |
| 3 | 4 | |
| 4 | 3 | |
| 6 | 2 | |
| 16 | 4 | 4 |
| 20 | 4 | 5 |
| 5 | 4 | |
| 24 | 4 | 6 |
| 6 | 4 | |
| 28 | – | – | 32 | – | – |
| 36 | 6 | 6 |
以上より、4の倍数となる場合の数は15通りとわかります。
(1)の結果から、2つのサイコロの目の和が8となる場合の数は5通りで、(2)の結果から、目の積が8となる場合は2通りであることがわかっています。これらに重複する目の出方がないため、単純にこれらを足せば答えが得られます。
したがって求める答えは7通りです。
練習問題2
(1) 代表を2人選ぶ方法は何通か?
(2) 2人を選ぶ際に、男女1人ずつとする場合は何通か?
(3) 3人を選ぶ際に、少なくとも1人は女子である場合は何通か?
単純に2人を選ぶ場合なので、全員(9人)の中から2人を選ぶ場合の数です。選ぶ順番は関係ないので組み合わせの公式より、
$$_9C_2 = \frac{9 \times 8}{2 \times 1} = 36(通り)$$
解き方1
男子を1人選ぶ場合の数は4通り、女子を1人選ぶ場合の数は5通りです。よって、これらを掛け合わせて
$$4 \times 5 = 20(通り)$$
解き方2
全員の中から2人を選ぶ場合の数から、2人とも男子となる場合の数と、2人とも女子となる場合の数を除けば、自ずと男女1人ずつ選んだ時の場合の数が求まります。
2人とも男子となる場合の数は、
$$_4C_2 = \frac{4 \times 3}{2 \times 1} = 6(通り)$$
2人とも女子となる場合の数は、
$$_5C_2 = \frac{5 \times 4}{2 \times 1} = 10(通り)$$
したがって、男女1人ずつ選ぶときの場合の数は、
$$36 – 6 – 10 = 20(通り)$$
性別に関係なく3人を選ぶときの場合の数は、
$$_9C_3 = \frac{9 \times 8 \times 7}{3 \times 2 \times 1} = 84(通り)$$
少なくとも1人が女子である場合の数は、全体の場合の数から3人とも男子の場合の数を引くことで求められます。3人とも男子(女子が1人も選ばれない)である場合の数は、
$$_4C_3 = _4C_1 = 4(通り)$$
したがって、
$$84 – 4 = 80(通り)$$
求める場合の数は80通りであることが計算できます。
練習問題3
(1) 1回目と4回目が表である場合の数
(2) 表が3回でる場合の数
1回目と4回目は表であることが確定しているので、コインの面の出方は、
表,?,?,表
となります。この分かっていない2回目と3回目の出方だけを考えればいいので、
$$2 \times 2 = 4(通り)$$
したがって、求める場合の数は4通りです。
解き方1
3回表が出るのは以下のような場合です。
| 1回目 | 2回目 | 3回目 | 4回目 |
|---|---|---|---|
| 表 | 表 | 表 | 裏 |
| 表 | 表 | 裏 | 表 |
| 表 | 裏 | 表 | 表 |
| 裏 | 表 | 表 | 表 |
したがって、求める場合の数は4通りです。
解き方2
4回のうち3回が表ということなので、組み合わせの公式より、
$$_4C_3 = 4(通り)$$
したがって、求める場合の数は4通りです。
練習問題4
(1) B と C が隣り合う場合
(2) A と C が両端に置かれる場合
[解き方1] B, Cの入り方を地道に数える
B と C が隣り合うときの並べ方を数えると、以下の8通りだとわかります。
BC◯◯◯
◯BC◯◯
◯◯BC◯
◯◯◯BC
CB◯◯◯
◯CB◯◯
◯◯CB◯
◯◯◯CB
◯には残りの3文字を当てはめれば良いですね。
残りの文字を◯に当てはめる場合の数は、3つの文字を一列に並べる順列と考えることができます。
なので、それぞれの並び方に対して、
$$3! = 3 \times 2 \times 1 = 6(通り)$$
これが8パターンあるので
$$6 \times 8 = 48(通り)$$
答えは48通りとわかります。
[解き方2] B, Cを一つのグループとして考える
B と C をくっついた1文字と考えます。すると、4つの文字([BC]という文字と、残りのA, D, E)を並べる順列と見なせます。
[BC]◯◯◯
従って並べ方は、
$$4! = 4 \times 3 \times 2 \times 1 = 24(通り)$$
そして、[BC]の中での並び方が2通り([BC]と[CB])があるので、
$$24 \times 2 = 48(通り)$$
答えは48通りとわかります。
A と C が両端に置かれるのは以下のような並べ方の時です。
A◯◯◯C
C◯◯◯A
残りの文字を◯に当てはめれば答えがでます。当てはめ方は3つの文字を一列に並べる順列と見なせるので、
$$3! \times 2 = 6 \times 2 = 12(通り)$$
よって答えは12通りです。
練習問題5
赤、青、緑、黄のインクを使って図の A, B, C, D の領域に色をつけたい。
(1) 同じ色を何度でも使っていい場合、何通の塗り方があるか?
(2) 4色全てを使って塗り分ける場合、何通の塗り方があるか?
(3) 3色を使って塗り分ける場合、何通の塗り方があるか。ただし、1色だけ2回使ってよいとする。
同じ色を何度でも使えるので、各領域に4色の塗り方ができます。したがって、これは重複順列と考えられます。
$$4 \times 4 \times 4 \times 4 = 4^4 = 256(通り)$$
4つのものを一列に並べる順列と考えられます。$$_4P_4 = 4! = 24(通り)$$
赤を2回使うとする。赤で塗りつぶす領域の選び方は、4つの領域から2つを選ぶ組み合わせの場合の数なので、
$$_4C_2 = \frac{4 \times 3}{2 \times 1} = 6(通り)$$
実際に全て書きだしてみると、以下のような6通りの塗り方があることがわかります。
| A | B | C | D |
| 赤 | 赤 | ◯ | ◯ |
| 赤 | ◯ | 赤 | ◯ |
| 赤 | ◯ | ◯ | 赤 |
| ◯ | 赤 | 赤 | ◯ |
| ◯ | 赤 | ◯ | 赤 |
| ◯ | ◯ | 赤 | 赤 |
◯に残りの3色から2色を選んで塗れば良いので、一つの並べ方につき、
$$_3P_2 = 3 \times 2 = 6(通り)$$
以上から、赤を2回使う場合の塗りつぶし方は全部で、
$$6 \times 6 = 36(通り)$$
これが残りの3色(青、緑、黄)を2回使う場合でも同じように考えられるので、全ての場合の数は、
$$36 \times 4 = 144(通り)$$
以上から、答えは144通りです。