Table of Contents
今回から少し変わった場合の数を求める問題を見ていきましょう。今回は重複順列についてです。
重複順列とは、簡単に言えば、1度使ったものを再び使うことのできる順列です。具体例を見ていきましょう。
例題1
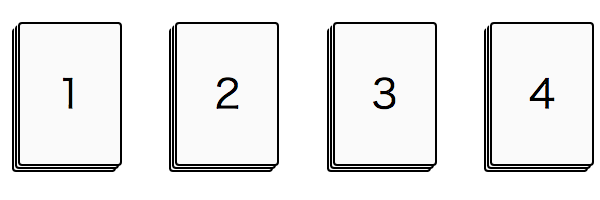
以下のような4種類の数字カードの山がある。これらのカードを使って4桁の数字を作るとすると、何通の数字が作れるか。ただし、一種類のカードを何度でも使って良いとする。
以前解いた順列の問題に似ていますが、決定的に違う点があります。それは、同じカードを何度でも使える点です。
カードが1枚しかなく、再度使うことができない場合は「1のカードを使ったら残りは2、3、4のどれか」と考えることができましたが、今回は1のカードを使っても、また1を使うことができます。
さて、この問題は4桁の数が何種類できるかを聞いていますので、各桁の数字カードの選び方を考えればいいですね。
次のように考えることができます。
| 1桁目 | 1, 2, 3, 4のいずれかを一つ選ぶ(4通りの選び方) |
| 2桁目 | 1, 2, 3, 4のいずれかを一つ選ぶ(4通りの選び方) |
| 3桁目 | 1, 2, 3, 4のいずれかを一つ選ぶ(4通りの選び方) |
| 4桁目 | 1, 2, 3, 4のいずれかを一つ選ぶ(4通りの選び方) |
つまり、どの桁でもカードの選び方は4通りとなります。したがって答えは、これらを掛け合わせるだけで求められます。
重複順列の基本的な考え方は以上です。それでは練習問題をいくつか解いてみましょう。
練習問題1
コインを5回連続で投げたときのコインの面の出方(表、表、裏、裏、表 など)は何通か?
コインは投げるたびに表か裏のどちらかが現れます。よって、2つの面から1つを選ぶことを5回繰り返すと言い換えることができます。したがって、
$$2 \times 2 \times 2 \times 2 \times 2 = 2^5 = 32(通り)$$
のコインの面の出方があります。
練習問題2
コインを4回連続で投げたときの面の出方で、一方の面しか出ない時を除いた出方は何通か?
ちょっとした応用問題です。まず一つの面しか出ない場合が何通か調べてみると…
(表、表、表、表)
(裏、裏、裏、裏)
となる場合の2通りですね。つまり、これ以外のコインの面の出方を数えればいいのですが、一つづつ数えるのは大変です。
なので、すべての面の出方を調べてから、上の2通りの出方だけを除外するという考え方をしたほうが簡単です。
すべての面の出方は…
$$2 \times 2 \times 2 \times 2 = 2^4 = 16(通り)$$
なので、求める場合の数は
(すべての面の出方) − (一つの面しか出ない場合) = 16 – 2 = 14(通り)
練習問題3
以下のような4種類の数字カードの山がある。これらのカードで1を最低1回は含む4桁の数字を作るとすると、何通の数字が作れるか。ただし、一種類のカードを何度でも使って良いとする。
今回は、1のカードを最低一回は使うという条件があります。
逆に、1のカードを全く使わない数字の場合を調べ、それをすべての場合から除外すれば、求めたい場合の数がわかります。
1のカードを全く使わない4桁の数字の作り方は、
$$3 \times 3 \times 3 \times 3 = 3^4 = 81(通り)$$
1も含め、4桁の数を作る場合の数は
$$4 \times 4 \times 4 \times 4 = 4^4 = 256(通り)$$
したがって答えは
256 – 81 = 175(通り)
以上の計算からもわかるように、同じものを繰り返し使える場合、異なるn個のものからr個のものを選んで並べる場合の数は次の式で求められます。
$$n^r$$
これは重複順列の公式と言えます。