Table of Contents
半径の長さと、中心角が弧度法(ラジアン)で与えられたときの扇形の円弧の長さと面積を求める方法についてです。
扇形の弧の長さを計算する
半径の長さと中心角の大きさから、扇の弧の長さを求める以下のような公式があります。
$$扇の弧の長さ = 半径の長さ \times 中心角$$
扇の弧の長さを $l$、半径の長さを $r$、中心角を $\theta$ とすると、
$$l = r\theta$$
となります。
この公式がなぜ成り立つかを詳しく紹介します。
ラジアンの定義
ラジアンとは、角度の大きさを、円周の長さとの関係で表すための考え方です。
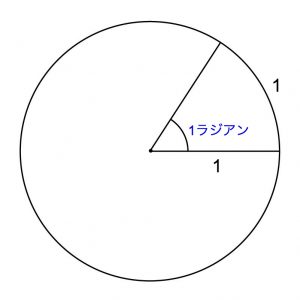
1ラジアン の定義は「半径 1 の円の、弧の長さが 1 の部分の扇の中心角」でした。
ラジアンの詳しい定義については以下の記事を御覧ください。
逆に言えば、この定義から、半径が 1、中心角が 1ラジアン の扇形の弧の長さは 1 です。
半径を変えてみる
では、半径が 2、中心角が 1ラジアン の扇形の弧の長さはいくつになるでしょうか。
半径が 2 の円は、半径が 1 の円の2倍の直径を持ちます。
円周の長さは以下の計算で決まりますので、直径の長さが2倍ということは、円周の長さも2倍になります。
$$円周の長さ = 直径 \times 円周率$$
円周率は不変($\pi = 3.14\cdots$)ですので、直径が2倍になれば、円周の長さも2倍になると言えます。
したがって、半径が 2、中心角が 1ラジアン の扇形の弧の長さは 2 です。
同じように考えると、円の半径が 3 であれば、中心角が 1ラジアン の扇形の弧の長さも 3、円の半径が $r$ であれば、中心角が 1ラジアン の扇形の弧の長さも $r$、というように、半径に比例して弧の長さも増加します。
中心角を変えてみる
それでは、中心角が変化した場合はどうなるでしょうか。
半径が 1、中心角が 2ラジアン の扇形の弧の長さは 2 です。これはラジアンの定義から明白です。
中心角が $\pi$ラジアン であれば、扇形の弧の長さも $\pi$、中心角が $2\pi$ラジアン であれば、もう扇形ではなく円となるため円周 $2\pi$ です。
半径が 1 の円(扇形)に関しては、中心角が $\theta$ であれば、扇形の弧の長さも $\theta$ であるということがわかります。
半径と中心角を両方変えてみる
上記の半径の変化による円弧の長さの変化と、中心角の変化による円弧の長さの変化は、双方に影響を及ぼす比例の関係にあります。
したがって、これらを掛け合わせることで扇の弧の長さを求めることができます。
$$扇の弧の長さ = 半径の長さ \times 中心角$$
扇の弧の長さを $l$、半径の長さを $r$、中心角を $\theta$ とすると、
$$l = r\theta\tag{1}$$
以上より、扇の弧の長さを求める公式が導きだせました。
練習問題1
答え
式(1)より、
$$l = 3 \times \frac{2}{3}\pi = 2\pi$$
練習問題2
答え
まず、度数法(°)で表されている中心角を弧度法(ラジアン)に変換します。
(詳しくは 弧度法(ラジアン)の定義と度数法への変換 を参照)
$$\theta = 60 \times \frac{\pi}{180} = \frac{\pi}{3}$$
式(1)より、
$$l = 5 \times \frac{\pi}{3} = \frac{5}{3}\pi$$
扇形の面積を計算する
半径の長さ $r$ と中心角の大きさ $\theta$ から、扇の面積 $S$ を求める以下の公式があります。
$$S = \frac{1}{2}r^{2}\theta\tag{2}$$
$\theta = 2\pi$ とすると、おなじみの円の面積の式となります。
$$S = r^{2}\pi$$
弧の長さを求める式(1)を利用すると、この式(2)は以下のように変形できます。
$$S = \frac{1}{2}rl$$
この式から、扇形の面積は、円弧の長さと半径をかけたものの半分に等しいと言えます。
練習問題3
答え
式(2)より、
$$S = \frac{1}{2} \times 6^{2} \times \frac{4}{5}\pi = \frac{72}{5}\pi$$
以上が扇形の弧の長さとその面積の求め方でした。