弧度法（ラジアン）の定義と度数法への変換

プログラムで角度や三角関数を扱うとき、場合によっては弧度法（ラジアン）と度数法（°）を使い分ける必要があります。

今回は、弧度法の定義と、それを度数法へ変換するための考え方について紹介します。

弧度法（ラジアン）の定義

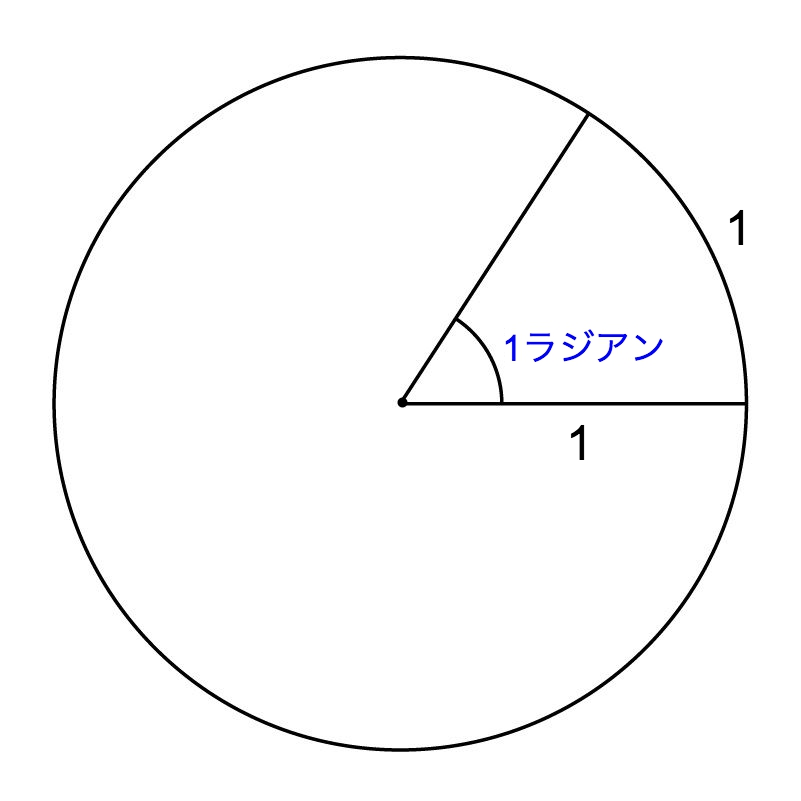
1ラジアンの定義は「半径が1の円の、弧の長さが1の部分（扇）の中心角」です。

図で表すと以下の部分の角度になります。

大体 $57^{\circ}$ です。これが正しいかどうか、これから検証してみましょう。

ラジアンを度数に変換

1ラジアンが度数法では何度（°）か求めてみましょう。

円の円周の長さは以下の式で求められます。

$$直径 \times 円周率$$

円周率 $3.14\cdots$ を $\pi$ とすると、

$$直径 \times \pi$$

半径1の円の直径は 2 ですので、その円周の長さは以下のように計算できます。

$$2 \times \pi = 2\pi$$

この全円周に対する中心角は、当然 360° です。

ここで、ラジアンの定義を考えてみると、円周の長さが1の部分に対する中心角ですので、求める度数を $x$ とすると、次の比の式が成り立ちます。

$$2\pi : 360 = 1 : x$$

円の円周の全長に対する中心角は 360° です。これと、円周の長さが 1 に対する中心角の比率は同じはずです。

したがって、1ラジアンは対する角度（°）は次の式で表すことができます。

$$x = \frac{360}{2\pi} = \frac{180}{\pi} \fallingdotseq 57^{\circ}$$

以上より、1ラジアンは大体 $57^{\circ}$ であることが計算できました。

同じように考えると、ラジアンから角度に変換するには、以下の使えばいいことがわかります。

$$角度（^{\circ}） = ラジアン \times \frac{180}{\pi}\tag{1}$$

例1

答え

$$0.18 \times \frac{180}{\pi} = \frac{32.4}{\pi} \fallingdotseq 10^{\circ}$$

角度からラジアンに変換

式（1）を変形すると、逆に角度からラジアンを求めるための式が導き出せます。

$$ラジアン = 角度（^{\circ}） \times \frac{\pi}{180}$$

この式によって度数からラジアンを求めることができます。

例2

答え

$$45 \times \frac{\pi}{180} \fallingdotseq 0.785$$

このように、ラジアンの定義を覚えておけば、度数とラジアンの相互変換を簡単に考えることができます。