Table of Contents
樹形図を使ってパターンを数える
さて、前回はサイコロを使った問題で場合の数を求める練習をしました。
今回は少し複雑な場合の数を求める問題を解いてみましょう。
カードを使った練習問題
今回は、1から4までの数字が書かれた4枚のカードを使った問題を例にします。
それでは早速問題です。
練習問題1
上の4枚のカードから2枚選んで、2桁の数字を作りたい。全部で何通りの数字を作ることができるか?
さて、カードを2枚選ぶとのことなので、とりあえず10の位(2桁目)にするカードを選んでみましょう。
この選び方は4通りですね。
1を選んだ場合
まず「1」を選んだとしましょう。
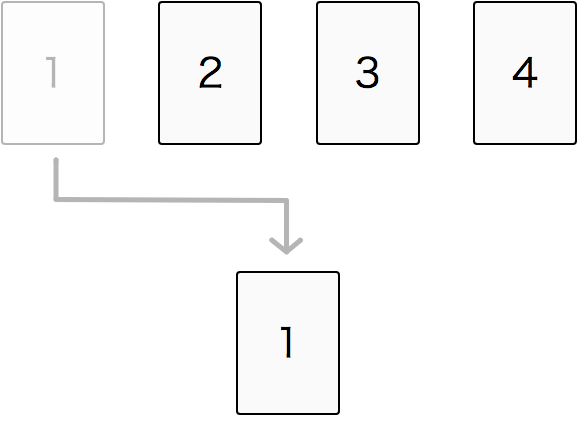
一度選んだカードはもうありませんので、2枚目のカードは残りの2, 3, 4のから選ぶことになります。
したがって、10の位に「1」を選んだときにできる2桁の数字は
12, 13, 14
の3通りということになります。
2を選んだ場合
それでは、初めに「2」を選んだ場合はどうでしょうか。
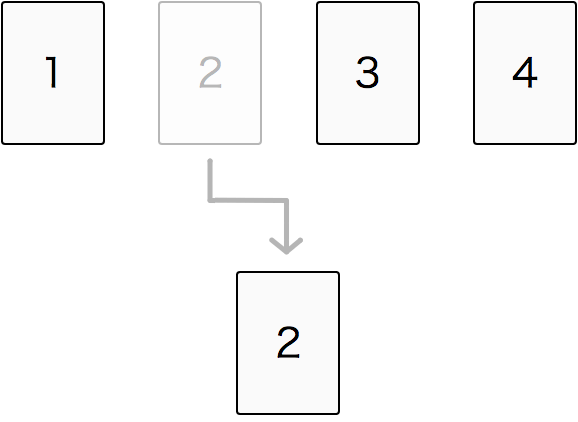
この場合も、1の位に選べるカードは「2」以外の3つですので、できる2桁の数字は、
21, 23, 24
となります。
同じように考えると、「3」や「4」を初めに選んだ場合も、2桁の数字の作り方はそれぞれ3パターンです。
31, 32, 34
41, 42, 43
以上のことから、4枚のカードから2枚選んで、2桁の数字を作る場合の数は
4 × 3 = 12(通り)であるとわかります。
場合の数が増えてきたら?
それでは、次の問題です。
練習問題2
上の4枚のカードから3枚選んで、3桁の数字を作りたい。全部で何通りの数字を作ることができるか?
ちょっと複雑になってきましたね。このように出来るもののパターンが増えてくると、頭の中だけで考えるのが大変になってきます。
そこで、樹形図という起こり得るパターンを図に書き出したものを利用すると、状況を整理しやすくなります。
実際に100の位(3桁目)に「1」を選んだ場合の樹形図を書いてみると、次のようになります。
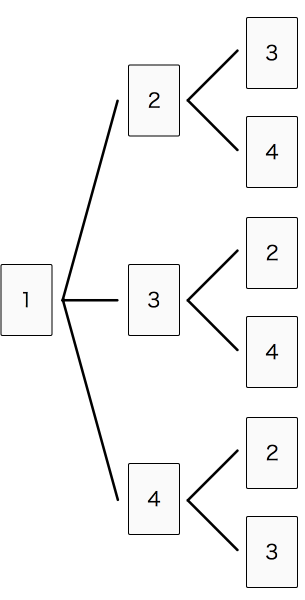
この図から、はじめに1を選んだときに出来る3桁の数字は
123, 124, 132, 134, 142, 143 の6通りということがわかります。
同じように考えて、他のカードが3桁目だった場合の場合の数も求められます。
以上より、この問題の答えは
4 × 6 = 24(通り)です。
練習問題3
最後に練習問題です。
上の4枚のカードすべてを使って4桁の数字を作りたい。全部で何通りの数字を作ることができるか?
3桁の数字を作った時点で、残っているカードは1枚しかありません。
つまり、3桁を作る場合と同じく 24通り となります。
もし取り得る数が膨大で、すぐには数えられないという場合は、このように樹形図を使って考えてみるとわかりやすくなることがあります。
次回は、場合の数を簡単に求められる公式と、その使い方について解説したいと思います。
