Table of Contents
近年、素粒子を利用した量子通信の実用に向けた動きが活発化しています。
素粒子は量子力学で記述される分野ですが、その理解には古典物理学の知識が必要となります。量子通信は電子のスピンを利用したものですので、電子(荷電粒子)の回転によって発生する磁気モーメントなどが関わってきます。磁気モーメントを理解するためには、力学における「力のモーメント」について理解しておく必要があります。
今回は、これらの概念の基礎となる「力のモーメント」及び「角運動量」について紹介します。
力のモーメントとは
力のモーメントは、物体を回転させようとする働きを表す量です。回転能率とも呼ばれます。身近なものでは「てこの原理」に関わります。
力のモーメント(Moment of force)とは,任意の回転軸(axis of rotation)のまわりに物体を回転させる効果を表す量であり,力の大きさ F と回転軸から力の作用線(line of action of force)までの距離(うでの長さ) h の積で決まる.
金沢工業大学 KIT物理ナビゲーション 力のモーメント
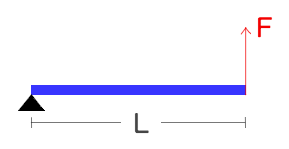
例えば、ある長さ $L$ の棒の片方の端を支点として、もう片方の端に力 $F$ を棒に対して垂直に加えたとすると、
$$L \times F = LF$$
という力のモーメントが働きます。
この式から同じ力でも回転軸から遠くにかかるほど物体を回転させる作用が強いということがわかります。
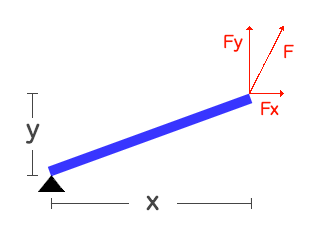
棒に対して垂直以外の力が働く場合は、以下のようにxy平面を考え、各方向の力のモーメントに分割すると考えやすいです。
この棒にかかる反時計回りの力のモーメント $N_1$ は、
$$N_1 = xF_y$$
時計回りの力のモーメント $N_2$ は、
$$N_2 = yF_x$$
となる。反時計回りの力のモーメントを正とすると、全体の力のモーメント $N$ は次のようになります。
$$N = N_1 – N_2 = xF_y – yF_x\tag{1}$$
角運動量とは
角運動量は、運動量のモーメントのことです。これを証明してみます。
運動量は、質量(重さ)と速度の積です。速度については以下の記事をご覧ください。
例えば、質量 $m$ の物体が速度 $\boldsymbol{v}$ で移動しているとすると、この物体の運動量 $p$ は以下のようになります。
$$\boldsymbol{p} = m \cdot \boldsymbol{v} = m\boldsymbol{v}$$
速度と運動量はベクトルなので太字で表しています。
角運動量と力のモーメントの関係
簡単化のため、2次元平面(xy平面)で考えます。
xy平面上にある質点(質量をもった微小点)があるとします。これがx軸方向の正の向きに $F_x$、y軸方向の正の向きに $F_y$ の力を受けて、x軸方向の運動量が $p_x$、y軸方向の運動量が $p_y$ となる運動をしているとします。
この状況でのx軸方向とy軸方向の運動方程式は、それぞれ以下のようになります。
$$\frac{dp_x}{dt} = F_x\tag{2}$$
$$\frac{dp_y}{dt} = F_y\tag{3}$$
この2つの式から、上記の式(1)の右辺と同じ式を作ることで、力のモーメントと運動方程式を関連付けることができます。
式(3)の両辺をx倍した式から、式(2)の両辺をy倍した式を引くと、
$$x\frac{dp_y}{dt} – y\frac{dp_x}{dt} = xF_y – yF_x$$
$$x\frac{dp_y}{dt} – y\frac{dp_x}{dt} + \frac{dx}{dt}p_y – \frac{dy}{dt}p_x = xF_y – yF_x$$
ここで、この式の第3項の第4項は以下のように変形できます。
$$\frac{dx}{dt}p_y – \frac{dy}{dt}p_x = v_xmv_y – v_ymv_x = 0$$
したがって、
$$x\frac{dp_y}{dt} – y\frac{dp_x}{dt} + 0 = xF_y – yF_x$$
$$x\frac{dp_y}{dt} – y\frac{dp_x}{dt} = xF_y – yF_x$$
$$\frac{d}{dt}(xp_y – yp_x) = xF_y – yF_x\tag{4}$$
この式の右辺は、上記の通り、xy平面の原点を回転軸とした場合の力のモーメントを表す式です。
左辺の括弧内は、これと同じ形をしていますが、力 $F$ ではなく運動量 $p$ となっています。したがって、これは運動量のモーメントと考えることができます。この部分を角運動量と呼びます。
括弧の中(角運動量)を $M$ とすると、式(1)と式(4)より、
$$\frac{dM}{dt} = N$$
したがって、角運動量の変化量(微分)は、力のモーメントに等しいことがわかります。今回は2次元平面上で考えましたが、3次元空間でも同様です。
おしまい
力のモーメントと角運動量とには関係性があることがわかりました。
これらのことが、素粒子の振る舞いを考える上でどのように役立つのかは後ほど紹介できればと思います。
参考: 森北出版株式会社 為近和彦 力学