Table of Contents
数学の集合論の問題の解き方と解説です。SPI試験の非言語問題としても出題される分野です。
例題1
| 科目 | 合格者数(人) |
|---|---|
| A | 34 |
| B | 26 |
(1)両方の試験に合格した人数が18人であるとき、どちらとも不合格だったのは何人か?
(2)両方の試験に合格した人数は、何人以上何人以下か?
考え方
このような問題は、ベン図(ヴェン図)を書くと考えやすくなります。
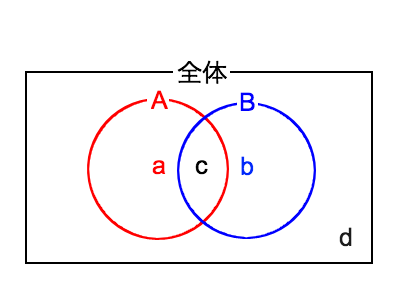
ベン図とは、以下のように、各条件に当てはまるものの数がどれだけになるかを視覚的に確認できる図です。
その名前は、ベン図の創始者とされるジョン・ヴェン(1834〜1923)から付けられているとされます。
(参考: 筑波大学 人文社会系 集合演算とヴェン図 橋本康二)
このベン図の各部に数値を当てはめていきます。
今回の問題では、50人が全体、科目Aに合格した34人が aとcを合わせた部分、科目Bに合格した26人が bとcを合わせた部分、どちらとも合格した人数が cの部分のみ、そして、どちらとも不合格だった人数が円の外側の部分 d となります。
科目Aだけに合格した人数は aの部分のみ、科目Bだけに合格した人数は bの部分のみ、となります。
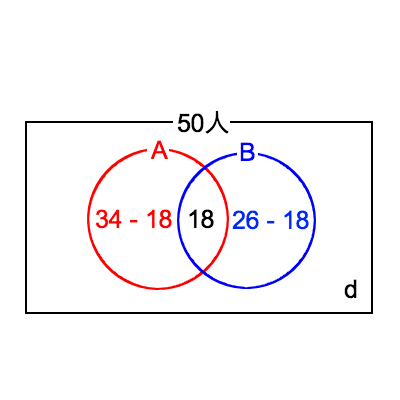
(1)では、両方とも合格した人数が18人、つまり $c = 18$ とわかっているので、図を以下のように書くことができます。
(1)で求めるべきものは d の部分にあてはまる数です。
これを求めるためには、全体の人数から円Aと円Bにあてはまる人数を引けば良いことがこのベン図からわかります。
それでは、実際に計算してみましょう。
円Aの全体(試験Aに合格した人数)が34人で、そのうち試験Bも合格している人は18人います。
円Bの全体(試験Bに合格した人数)が26人で、そのうち試験Aも合格している人は18人います。
つまり、試験Aだけに合格している人数は $34 – 18 = 16$ です。(ベン図では a から c を除いた領域)
同様に、試験Bだけに合格している人数は $26 – 18 = 8$ です。(ベン図では b から c を除いた領域)
したがって、2つの円の領域にあてはまる人数は、以下のように計算できます。
$$16 + 8 + 18 = 42$$
よって、円Aと円Bを合わせた人数は 42人 であることがわかりました。
全体の人数からこの人数を引けば、どちらとも不合格だった人数がわかります。
$$50 – 42 = 8$$
以上より、両方の試験ともに不合格だったのは8人であることがわかりました。
(2)は、c の数が不明で、ここに当てはまり得る人数の範囲を求める問題です。
仮に、この領域c(両方の試験に合格した人数)が 0 だとすると、ベン図は以下のようになります。
しかし、このベン図は、円の中の人数が全体よりも多くなってしまっており、明らかに誤りです。
数値でいうと、試験Aに合格した人数(34人)と試験Bに合格した人数(26人)を足して60人となり、これは全体の50人より10人多くなってしまっています。
つまり、最低でも10人は両方の試験に合格していると言えます。
今度は、試験Bを合格した人全員が、試験Aも合格していると仮定してみます。この場合、ベン図は以下のようになります。
この図は、どちらとも不合格の人数(d)が16人となればあり得ることです。
したがって、両方の試験を合格する最大の人数は26人と言えます。
以上より(2)の答えは、10人以上26人以下であると言えます。
練習問題1
スイカが嫌いな人数の最大値は、
$$36 – 18 = 18(人)$$
メロンが嫌いな人数の最大値は、
$$36 – 16 = 20(人)$$
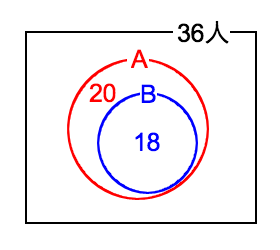
つまり、どちらも嫌いな生徒の人数の最大値は 18人 となります。嫌いな人数についてベン図を使って書くと以下のようになります。
(Aが「メロンが嫌いな人数」、Bが「スイカが嫌いな人数」を表します)
どちらも嫌いな生徒の人数が最小となる場合は、このベン図における2つの円がなるべく重なり合わない状態となります。完全に円を離した場合、2つの円に含まれる人数の合計は以下のようになります。
$$18 + 20 = 38(人)$$
しかし、このように完全に離れてしまっては、全体の人数である36人を超えてしまうことになります。
よって最低でも以下の人数は、どちらとも嫌いでなければいけません。
$$38 – 36 = 2(人)$$
以上より、どちらも嫌いな生徒は2人以上18人以下となります。